Site menu:

Berechnung von Effektstärken
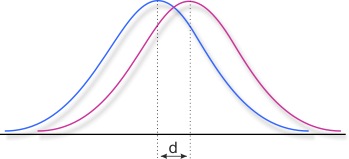
Statistische Signifikanz besagt, ob ein Ergebnis unter Berücksichtigung eines Restrisikos noch durch Zufall zustande gekommen sein kann, oder nicht. Nicht jedes statistisch signifikante Ergebnis ist jedoch auch praktisch bedeutsam. Je nachdem, wie viele Daten zur Verfügung stehen, welches Datenniveau diese haben und welche Analysemethoden zur Anwendung kommen, sind auch kleine Effekte unter Umständen statistisch signifikant, obwohl sie in der Realität kaum bemerkbar sind. Zur Einschätzung der praktischen Bedeutsamkeit existieren verschiedene Effektstärkemaße, die bei der Interpretation der Größe eines Effektes helfen. Die bekannteste ist die Effektstärke d von Cohen (1988), die ein Maß für den standardisierten Mittelwertsunterschied zweier Gruppen ist.
Es gibt jedoch noch viele andere Maße. Im folgenden finden Sie eine Reihe an Berechnungsmöglichkeiten, Umrechnungen zwischen Effektstärken und eine Interpretationstabelle. Bitte klicken Sie den jeweiligen Balken an, um den zugehörigen Rechner auszuklappen:
Handelt es sich um zwei Gruppen mit gleicher Gruppengröße, so kann aus Mittelwert 1 und Mittelwert 2 sowie der jeweiligen Standardabweichung die Effektstärke dCohen berechnet werden. Dabei wird die gepoolte Standardabweichung zugrunde gelegt. Diese Effektstärke wird beispielsweise bei einem Vergleich zweier verschiedener Gruppen in einem Experiment angewandt. Für Prä-Post-Designs einer Gruppe empfiehlt sich aufgrund der Abhängigkeit der Daten eher die Verwendung von Rechner 4 oder 5.
Sind die Standardabweichungen beider Gruppen sehr unterschiedlich, so schlägt Glass vor, nicht auf die gepoolte Standardabweichung zurückzugreifen, sondern auf die Standardabweichung der Kontrollgruppe. Dahinter steckt die Logik, dass die Standardabweichung der Kontrollgruppe nicht durch eine Intervention beeinflusst wurde. Das Effektstärkemaß wird als Glass' Δ ("Glass' Delta") bezeichnet. In der folgenden Tabelle wird für die Berechnung von Glass' Δ davon ausgegangen, dass es sich bei Gruppe 1 um die Kontrollgruppe handelt.
Zusätzlich wird die Common Language Effect Size (CLES; McGraw & Wong, 1992) ausgegeben, die eine non-parametrische Effektstärke darstellt. Sie gibt die Wahrscheinlichkeit an, dass ein zufällig aus der einen Stichprobe gezogener Fall einen höheren Wert hat als als ein zufällig gezogener Fall aus der anderen Stichprobe. In diesem Rechner wird die Wahrscheinlichkeit aus Sicht der Gruppe mit dem höheren Mittelwert berichtet, aber der Bezugspunkt lässt sich umdrehen, indem man die Gegenwahrscheinlichekit (1 - CLES) berechnet.
| Gruppe 1 | Gruppe 2 | |
| Mittelwert | ||
| Standardabweichung | ||
| Effektstärke dCohen | ||
| Effektstärke Glass' Δ | ||
| Common Language Effect Size CLES | ||
| N (Gesamtzahl an Beobachtungen in beiden Gruppen) |
|
| Konfidenzkoeffizient | |
| Konfidenzintervall für dCohen |
Bitte beachten Sie, dass bei Interventionen ohne Kontrollgruppe, also einem einfachen Prä-Post-Design, sehr schnell sehr große Effekte entstehen können, diese aber nicht zwangsläufig auf die Intervention zurückführbar sind. Eine bessere Herangehensweise für den Nachweis von Effekten bei Interventionsstudien liegt im Vergleich der Effekte in der Experimental- und einer Kontrollgruppe (z. B. Wartelistenkontrollgruppe oder Alternativbehandlung).
Analog zu 1. lässt sich die Effektstärke bei unterschiedlicher Gruppengröße berechnen, indem die Größe der Gruppe bei der Berechnung der gepoolten Standardabweichung berücksichtigt wird. Der Ansatz ist im wesentlichen vergleichbar mit dCohen, außer dass die gepoolte Standardabweichung um einen kleinen, positiven Bias korrigiert wird. In der Literatur wird dieser Effekt sehr häufig ebenfalls als dCohen bezeichnet (siehe auch Anmerkung unterhalb der Tabelle).
Weiterhin wird die Common Language Effect Size (CLES; McGraw & Wong, 1992) ausgegeben, die eine non-parametrische Effektstärke darstellt. Sie gibt die Wahrscheinlichkeit an, dass ein zufällig aus der einen Stichprobe gezogener Fall einen höheren Wert hat als ein zufällig gezogener Fall aus der anderen Stichprobe. In diesem Rechner wird die Wahrscheinlichkeit aus Sicht der Gruppe mit dem höheren Mittelwert berichtet, aber der Bezugspunkt lässt sich umdrehen, indem man die Gegenwahrscheinlichekit (1 - CLES) berechnet.
Für die Effektstärke lässt sich zudem ein Konfidenzintervall berechnen, also einen Bereich, in dem bei Berücksichtigung der Variabilität empirischer Ergebnisse die Effektstärke mit einer bestimmten Wahrscheinlichkeit liegt (Berechnung nach Hedges & Olkin, 1985, S. 86). Falls Sie diese Berechnung möchten wählen Sie bitte die gewünschte Sicherheitswahrscheinlichkeit (= Konfidenzkoeffizient) aus. Das Intervall wird umso größer, je höher die Sicherheitswahrscheinlichkeit gewählt wird.
| Gruppe 1 | Gruppe 2 | |
| Mittelwert | ||
| Standardabweichung | ||
| Gruppengröße (N) | ||
| dCohen bzw. gHedges * | ||
| Common Language Effect Size CLES** | ||
| Konfidenzkoeffizient | |
| Konfidenzintervall |
* Anmerkung: Die Terminologie ist leider nicht einheitlich. Ursprünglich wurde die Größe g von Hedges und Olkin in Anlehnung an Cohen als d bezeichnet. g wurde dagegen Anfang der 80er für korrigierte Effektstärken verwendet, da Glass als erster Korrekturen vorgeschlagen hatte (siehe Ellis, 2010, S. 27). Aus diesem Grund hat sich für das Maß von Hedges in Anlehnung an Glass der Buchstabe g eingebürgert und nicht h, wie es dieser Logik folgend eigentlich sein müsste. In der Regel wird der Effekt aber ebenfalls schlicht mit dem Buchstaben d versehen.
**Die Common Language Effect Size (CLES) wird hier über die kumulative Wahrscheinlichkeit auf der Basis der korrigierten Effektstärke folgendermaßen berechnet:
Bei einer Interventionsstudie wird die Entwicklung von mindestens zwei verschiedenen Gruppen (i. d. R. eine Kontroll- und eine Experimentalgruppe) miteinander verglichen. Es gibt dabei verschiedene Möglichkeiten, wie mit Vortestunterschiedenen und unterschiedlichen Varianzen umgegangen werden kann. Klauer (2001) schlägt vor, die Effektstärken der Prä- und Postmessung mittels Hedges g zu berechnen und die beiden Effektstärken voneinander abzuziehen. Hierbei werden sowohl unterschiedliche Gruppengrößen, als auch Vortestunterschiede korrigiert. Die Berechnung basiert also auf der Differenz der Effektstärken beider Gruppen gemäß Berechnungsvariante 2. Morris (2002) stellt unterschiedliche Effektmaße für Designs mit Messwiederholung vor und kommt in seiner Modellrechnung zum Schluss, dass die Differenzen der Prä-Post-Messung in den Gruppen an der gepoolten Standardabweichung der Prä-Messung gewichtet werden sollte (sog. dppc2 nach Carlson & Smith, 1999), da diese durch die Intervention nicht beeinflusst wurde. Zudem werden verschiedene Gewichtungsfaktoren berücksichtigt. Das folgende Formular ermöglicht beide Berechnungsvarianten, die beide in den meisten Fällen zu sehr ähnlichen Ergebnissen kommen.
Der Nachteil beider Vorgehensweisen liegt darin, dass die verschiedenen Messzeitpunkte als unabhängige Gruppen betrachtet werden. Bitte beachten Sie deshalb auch Berechnungsvarianten 4 und 5, um basierend auf den Ergebnissen von Teststatistiken aus Hypothesentests die Abhängigkeiten zwischen Messzeitpunkten zu berücksichtigen. Alternativ können Sie auch bei Varianzanalysen die Effekte über den Anteil aufgeklärter Varianz (η2) in die Effektstärke d transformieren.
| Interventionsgruppe | Kontrollgruppe | |||
| Prä | Post | Prä | Post | |
| Mittelwert | ||||
| Standardabweichung | ||||
| Gruppengröße (N) | ||||
| Effektstärke dppc2 sensu Morris (2008) | ||||
| Effektstärke dKorr sensu Klauer (2001) | ||||
Während es bei den Abschnitten 1 bis 3 darum ging, die Werte unabhängiger Gruppen miteinander zu vergleichen, geht es v. a. in der Interventionsforschung darum, die Veränderungen in einer Gruppe zu erfassen. Morris und DeShon (2002, p.109) schlagen eine Korrektur vor, bei der die in der Berechnung der Effektstärke verwendete Standardabweichung korrigiert wird. In den Korrekturfaktor geht die Korrelation zwischen Prä- und Postmessung ein:
Werte von r = .5 führen zu den gleichen Effektstärken wie in der Berechnung des regulären dCohen. Höhere Werte führen dagegen zu größeren Effektstärken als der Vergleich zwischen unabhängigen Gruppen. Morris & DeShon (2008) empfehlen, als Standardabweichung den Wert des Prätests zu nehmen, da dieser Wert nicht durch die Intervention beeinflusst wurde und Parallelen zu Glass Δ aufweist. Die Effektstärke wird im Folgenden als dRepeated Measures (dRM) bezeichnet. Die zweite Effektstärke dRepeated Measures, pooled (dRM, pool) nutzt die gepoolte und anhand der Korrelation korrigierten Standardabweichung (vgl. Lakens, 2013, formula 8). Weiterhin stellt die einfache Mittelung der Standardabweichung einen häufig in der metaanalytischen Forschung genutzten Kennwert dar, der nach Cumming (2012) als dav bezeichnet wird und bei dem die Korrelation zwischen den Gruppen nicht berücksichtigt wird.
| Gruppe 1 | Gruppe 2 | |
| Mittelwert | ||
| Standardabweichung | ||
| Korrelation | ||
| dRM | ||
| dRM, pooled | ||
| dav | ||
N|
| |
| Konfidenzkoeffizient | |
| Konfidenzintervall für dRM |
Vielen Dank an Sven van As für den Hinweis zu dRM und an Tobias Richter für den Hinweis zu dav und der Publikation von Lakens (2013).
Effektstärken können nicht alleine nur aus Rohdaten, sondern auch aus Teststatistiken von Hypothesentests wie z. B. t-Tests gewonnen werden. Handelt es sich um unabhängige Gruppen, so ergeben sich im wesentlichen die gleichen Effektstärken wie bei Berechnungsvariante 2.
Beim abhängigen Testen von Hypothesen (z. B. bei Untersuchungen im Prä-Post-Design oder gematchten Stichproben) wird dagegen noch mehr Informationen ausgeschöpft, da die Zuordnung von Datenpunkten zwischen zwei Messungen erhalten bleibt, also beispielsweise die Ergebnisse einer Person oder auch die Zuordnung von z. B. Zwillingen oder gematchten Personen. Entsprechend wird auch bei der Berechnung von Effektstärken mehr Information berücksichtigt. Diese Vorgehensweise entspricht im wesentlichen dem Vergleich von Prä-Posttest-Differenzen und deren Testung mittels eines unabhängigen T-Tests (Morris & DeShon, 2002, p. 119) und sollte dementsprechend ähnliche Effektstärken erzielen.
Bitte wählen Sie zur Berechnung, ob es sich um einen abhängigen oder unabhängigen Test handelt und geben Sie die Prüfgröße t an. Geben Sie für den abhängigen Test zusätzlich die Anzahl an Fällen und die Korrelation zwischen beiden Variablen an. Spezifizieren Sie beim unabhängigen Test die Größe der beiden Gruppen. Die Berechnung erfolgt nach Borenstein (2009, S. 228f.).
| Testung | |
| t-Wert | |
| n1 | |
| n2 | |
| r | |
| Effektgröße d | |
* Für die Berechnung für die Formel tc aus Dunlop, Cortina, Vaslow & Burke (1996, S. 171) verwendet, da diese gemäß Simulationsrechnungen beste Schätzung für die Effektstärke d darstellt:
Wir danken Frank Aufhammer für den Hinweis zu dieser Publikation.
Ein sehr einfaches Maß zur Ermittlung des Effekts ist bei Varianzanalysen das η2, das den Anteil an aufgelärter Varianz an der Gesamtvarianz darstellt. Dieser Anteil lässt sich auch in d umrechen. Steht die Angabe zum η2 nicht zur Verfügung, so kann auch aus dem F-Wert eine Effektstärke berechnet werden, sofern die Größe beider Gruppen bekannt ist. Die folgende Berechnung ist für Varianzanalysen mit zwei Gruppen (df1 = 1) vorgesehen. Die Berechnung erfolgt nach Thalheimer & Cook (2002):
| F-Wert | |
| Fallzahl der Treatment-Gruppe | |
| Fallzahl der Kontroll-Gruppe | |
| Effektgröße d |
Sind die Mittelwerte der verschiedenen Gruppen einer Varianzanalyse bekannt, so lassen sich hieraus die Effektstärken f und d berechnen (Cohen, 1988, S. 273 ff.). Allerdings muss hierfür selbst ein bisschen gerechnet werden: Bestimmten Sie zunächst die Gruppen mit dem maximalen und dem minimalen Mittelwert. Berechnen Sie die gepoolte Standardabweichung der einzelnen Gruppen σpool. Weiterhin muss entschieden werden, wie stark die Bandbreite der Mittelwerte variieren:
- Wählen Sie "minimale Variation", wenn die Gruppenmittelwerte mit Ausnahme des minimalen und maximalen Wertes nahe am Gesamtmittelwert liegen.
- Wählen Sie "mäßige Variation", wenn sich die Gruppenmittelwerte gleichmäßig über die ganze Bandbreite verteilen.
- Wählen Sie "maximale Variation", wenn sich die Gruppenmittelwerte nahe am minimalen und maximalen Mittelwert liegen, in der Mitte jedoch kaum.
| Höchster Mittelwert (mmax) | |
| Niedrigster Mittelwert (mmin) | |
| Mittlere Streuung σpool der Teilstichproben | |
| Anzahl an Gruppen | |
| Verteilung der Mittelwerte | |
| Effektgröße f | |
| Effektgröße d |
Effektstärken wie d oder Korrelationen sind oftmals nicht leicht zu kommunizieren. Nimmt man beispielsweise r2 als Maß für die aufgeklärte Varianz, so wirken Effekte rasch sehr klein. Wenn die entsprechenden Interpretationen nicht bekannt sind, so verdichtet sich der Eindruck, eine Intervention sei erfolglos. Aber auch kleine Effekte können sehr bedeutsam sein, insbesondere wenn es um existenzielle Fragen geht. Zwei Beispiele (vgl. Hattie, 2009):
- Der Effekt von Aspirin auf Herz-Kreislauferkrankungen liegt lediglich bei d = 0.07. In der Folge sterben jedoch 34 von 1000 Personen weniger an Herzinfarkten.
- Chemo-Therapien bei Brustkrebs haben lediglich einen Effekt von d = 0.12 und sind somit nach den Interpretationsratschlägen von Cohen praktisch vernachlässigbar. Trotzdem retten sie vielen Frauen das Leben.
Rosenthal und Rubin (1982) schlagen deshalb vor, die Effektivität von Interventionen über die Zunahme von Erfolgen auszudrücken. Die Vorgehensweise ist geeignet für 2x2-Kontingenztabellen, bei denen in den Zeilen die verschiedenen Gruppen (Interventionsgruppe versus Kontrollgruppe) und in den Spalten die Fallzahlen für Erfolg versus Misserfolg (z. B. geheilt versus nicht geheilt) notiert wird. Der BESD wird berechnet, indem man die Erfolgswahrscheinlichkeit der Behandlungsgruppe von der Erfolgswahrscheinlichkeit der Kontrollgruppe abzieht. Die Prüfgröße kann zudem in die Effektstärke nach dCohen umgerechnet werden.
Ein anderes, in der evidenzbasierten Medizin weit verbreitetes Effektstärkemaß ist das sog. Number Needed to Treat. Dieses veranschaulicht, wie viele Personen man in der Behandlungsgruppe benötigen würde, um im Vergleich zur Kontrollgruppe mindestens einen zusätzlichen Fall mit günstigem Ausgang beobachten zu können. Ist der Wert negativ, so spricht man von Number Needed to Harm, also von einer schädigenden Wirkung.
Bitte tragen Sie bei der Interventions- und der Kontrollgruppe die Fallzahlen für Erfolg und für Misserfolg ein:
| Erfolg | Misserfolg | Erfolgs- wahrscheinlichkeit |
|
| Interventionsgruppe | |||
| Kontrollgruppe | |||
| Binomial Effect Size Display (BESD) (Zunahme der Erfolgswahrscheinlichkeit) |
|||
| Number Needed to Treat | |||
| rPhi | |||
| Effektstärke dcohen | |||
Eine Konvertierung zwischen NNT und anderen Effektstärken wie Cohen's d ist nicht ohne weiteres möglich. Im obigen Beispiel wird versucht, die Effektstärke d über die punkt-biserale Korrelation rphi zu schätzen. Alternative Herangehensweisen (vgl. z. B. Furukawa & Leucht, 2011) ermöglichen es, auch eine Konvertierung von d zu NNT vorzunehmen. Die Ergebnisse stimmen innerhalb eines mittleren Bereichs von -1.0 ≤ d ≤ 1.0 im Wesentlichen mit der Konvertierung auf der Basis der Rohdaten überein:
| Cohen's d | Number Needed to Treat (NNT) |
Wenn es in einer Studie darum geht, ob ein Ereignis (z. B. Heilung) eintritt und ob sich zwei Gruppen in der Häufigkeit dieses Ereignisses unterscheiden, dann greift man in der Regel auf Odds Ratios, Risk Ratios und Risk Difference zurück (vgl. Borenstein et al. 2009, Kap. 5). Einen sehr häufigen Einsatz finden diese Effektstärkemaße deshalb in klinischen Studien und in der Epidemiologie. Die drei Maße haben die folgende Bedeutung:
- Risk Ratio oder Relatives Risiko: Es handelt sich schlicht um das Verhältnis zweier Risiken bzw. Wahrscheinlichkeiten, z. B. das Risiko zu sterben in der Treatment-Gruppe geteilt durch das Risiko in der Kontrollgruppe.
- Odds Ratio oder Quotenverhältnis: Das Odds Ratio ist mit dem relativen Risiko vergleichbar, nur dass hier Quoten berechnet werden. Ein Beispiel: Wenn es darum geht, zu untersuchen, wie viele Menschen versterben, dann teilt man nicht die Anzahl an Verstorbenen durch die Gesamtzahl der Personen einer Gruppe, sondern man berechnet das Verhältnis aus Verstorbenen und Überlebenden in der Gruppe. Wenn die Wahrscheinlichkeit für das untersuchte Ergeignis gering ist, dann sind beide Maße sehr ähnlich. Für viele Menschen sind Odds Ratios weniger intuitiv verständlich, verglichen mit dem relativen Risiko. Das Maß weist aber einige statistische Vorzüge auf, weswegen es in Metaanalysen meist bevorzugt wird. Ein auf Odds Ratios basierendes Maß ist auch Yule's Q bei dem das Odds Ratio auf den Bereich von -1 bis +1 normiert wird.
- Risk Difference oder Risikodifferenz: Hierbei handelt es sich einfach nur um die Differenz des Risikos in beiden Gruppen. Anders als beim relativen Risiko wird also nicht das Verhältnis des Risikos zwischen den Gruppen berechnet, sondern beide Werte werden voneinander abgezogen. Beim relativen Risiko wird ausschließlich mit den Rohdaten gearbeitet und die Werte nicht für die Berechnung von Varianz und Standardfehler logarithmiert. Anders als die anderen beiden Maße ist die Risikodifferenz anfällig gegenüber der absoluten Höhe der Grundrate eines Phänomens.
| Ereignis eingetreten |
Ereignis nicht eingetreten |
N | |
| Teatment | |||
| Kontrollgruppe | |||
|
| |||
| Risk Ratio | Odds Ratio | Risk Difference | |
| Ergebnis | |||
| Log | |||
| geschätzte Varianz V | |||
| geschätzter Standardfehler SE | |||
| Yule's Q | |||
Cohen (1988, S. 109) schlägt ein Effektstärkemaß mit der Bezeichnung q vor, das den Unterschied zweier Korrelationen interpretierbar macht. Bei dieser Vorgehensweise werden die beiden Korrelationen Fisher-Z-transformiert und von einander abgezogen. Cohen schlägt als Interpretation von q die folgende Einteilung vor: <.1: kein Effekt; .1 bis.3: kleiner Effekt; .3 bis .5: mittlerer Effekt; >.5: großer Effekt.
| Korrelation r1 | |
| Korrelation r2 | |
| Cohen's q | |
| Interpretation |
Insbesondere bei Metaanalysen ist es häufig notwendig, Korrelationen zu mitteln oder Signifikanztests mit Korrelationen (Testung auf unterschiedlichkeit, Testung auf Verschiedenheit von 0 ...) durchzuführen. Auf der Seite Signifikanztests bei Korrelationen finden Sie entsprechende Online-Rechner.
Für die Effektstärkemaße wie Cohen's d oder η2 sind Verteilungsannahmen notwendig. Werden diese nicht erfüllt, wie z. B. im Fall von ordninal- oder nominalskalierten Daten, dann wird meist auf non-parametrische Tests wie Wilcoxon oder Mann-Whitney-U zurückgegriffen. Die Verteilungen der Prüfgrößen dieser Testverfahren werden anschließend mittels z-Verteilung approximiert und entsprechend wird die Signifikanz bestimmt. Die Prüfgrößen können analog auch in eine Effektstärke umgerechnet werden (siehe Fritz, Morris & Richler, 2012, S. 12; Cohen, 2008). Im Folgenden können die Teststatistiken von Wilcoxon-Rangsummentest, Mann-Whitney-U oder Kruskal-Wallis-H zur Berechnung von η2 verwendet werden. Alternativ kann direkt auf die Prüfgröße z zurückgegriffen werden.
| Test | |
Teststatistik * |
|
n2 |
|
n2 |
|
| Eta squared (η2) | |
| dCohen** |
* Anmerkung: Bitte geben Sie als Prüfgröße bitte nicht die Rangsummen ein, die beispielsweise von SPSS ausgegeben werden, sondern verwenden Sie die Prüfgrößen U, W oder z der statistischen Tests. Bei Wilcoxon und Kruskal-Wallis ist die Gesamtstichprobengröße einzugeben. Geben Sie bei Kruskal-Wallis-H zusätzlich die Anzahl an Gruppen an. Sollten Sie die z-Statistik gewählt haben, so ist ebenfalls die Gesamtstichprobengröße einzugeben.
** Die Transformation von η2 nach d wird mit der Prozedur aus Umrechnung der Effektstärken d, r, η2, f und des Odds Ratio vorgenommen.
Studien, die auf der Regressionsanalysen basieren, sind schwer in metaanalytische Forschung einzubeziehen, wenn sie nur standardisierte β Koeffizienten angeben. Es wird diskutiert, ob eine Imputation in diesem Fall möglich und ratsam ist. Andererseits wird die Aussagekraft der Analysen reduziert, wenn zu viele Studien nicht einbezogen werden können, was wiederum die Repräsentativität der Ergebnisse verzerrt. Peterson und Brown (2005) schlagen ein Verfahren zur Umrechnung standardisierter β Gewichte in r vor, wenn die β-Gewichte zwischen -0.5 und 0.5 liegen. r kann dann direkt als Effektgröße verwendet oder in d oder andere Metriken umgerechnet werden. Peterson und Brown (2005, S. 180) empfehlen: "However, despite the potential usefulness of the proposed imputation approach, meta-analysts are still encouraged to make every effort to obtain original correlation coefficients."
| Standardized β weight | r | |
Zur Berechnung von Cohen's d, aber auch in anderen Zusammenhängen ist es notwendig, die mittlere (= gepoolte) Standardabweichung zu berechnen. Hier ein kleines Hilfsmittel, inkl. Korrektur unterschiedlicher Gruppengrößen für bis zu 10 Gruppen. Bitte geben Sie zunächst die Anzah an Gruppen an. Wenn Werte bei der Angabe der Gruppengrößen fehlen oder ungültig sind, dann wendet der Rechner keine Korrektur für Gruppengrößen an.
| Number of Groups | Standardabweichung (sd) | Stichprobengröße (n) |
| Gruppe 1 | ||
| Gruppe 2 | ||
| Gepoote Standardabweichung spool | ||
Bitte wählen Sie im Dropdown-Menü die Effektstärke, die Sie umrechnen möchten und geben Sie im Feld rechts daneben anschließend die betreffende Angabe ein. Die Umrechnung erfolgt nach Cohen (1988), Rosenthal (1994, S. 239), Borenstein, Hedges, Higgins, und Rothstein (2009; Umrechnung zwischen Odds Ratio und anderen Effektstärken) und Dunlap (1994; Berechnung des CLES).
| Effektstärke | ||
| d | ||
| r | ||
| η2 | ||
| f | ||
| Odds Ratio | ||
| Common Language Effect Size CLES | ||
| Number Needed to Treat (NNT) | ||
Die Effektstärkemaße d und r können aus den Prüfgrößen von χ2 und z aus Hypothesentests berechnet werden (Vorgehen nach Rosenthal & DiMatteo, 2001, S. 71; siehe auch Elis, 2010, S. 28). Das Vorgehen ist bezüglich des χ2-Tests nur bei Fällen mit einem Freiheitsgrad zulässig. Bitte wählen Sie im Dropdown-Menü die Prüfgröße aus und geben Sie den Wert ein. Spezifizieren Sie zusätzlich das N. Die Umrechnung in d und η2 erfolgt mit den Formeln der vorherigen Funktion.
| Prüfgröße | ||
| N | ||
| d | ||
| r | ||
| η2 | ||
Hier sehen Sie noch einmal im Überlick die Interpretation der Effektstärken nach Cohen (1988) und Hattie (2009 S. 97). Hattie legt seiner Einstufung real erreichbare Effekte im Bildungssystem zugrunde und kommt deshalb zu einer etwas milderen Einstufung. Dort wo die Intervallgrenzen nicht exakt in die tabellarische Auflistung passten, wurde jeweils zur nächsten Intervallgrenze der Angabe der Effektstärke d gerundet.
| d | r* | η2 | Interpretation nach Cohen (1988) | Interpretation nach Hattie (2009) |
| < 0 | < 0 | - | negativer Effekt | |
| 0.0 | .00 | .000 | kein Effekt | Developmental effects |
| 0.1 | .05 | .003 | ||
| 0.2 | .10 | .010 | kleiner Effekt | Teacher effects |
| 0.3 | .15 | .022 | ||
| 0.4 | .2 | .039 | Zone of desired effects | |
| 0.5 | .24 | .060 | mittlerer Effekt | |
| 0.6 | .29 | .083 | ||
| 0.7 | .33 | .110 | ||
| 0.8 | .37 | .140 | großer Effekt | |
| 0.9 | .41 | .168 | ||
| ≥ 1.0 | .45 | .200 | ||
* Cohen (1988) gibt für r die folgenden Intervalle an: .1 bis .3: kleiner Effekt; .3 bis .5: mittlerer Effekt; .5 und höher: starker Effekt
Borenstein (2009). Effect sizes for continuous data. In H. Cooper, L. V. Hedges, & J. C. Valentine (Eds.), The handbook of research synthesis and meta analysis (pp. 221-237). New York: Russell Sage Foundation.
Borenstein, M., Hedges, L. V., Higgins, J. P. T., & Rothstein, H. R. (2009). Introduction to Meta-Analysis, Chapter 7: Converting Among Effect Sizes . Chichester, West Sussex, UK: Wiley.
Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2. Auflage). Hillsdale, NJ: Erlbaum.
Cohen, B. (2008). Explaining psychological statistics (3rd ed.). New York: John Wiley & Sons.
Cumming, G. (2012). Understanding the New Statistics: Effect sizes, Confidence Intervals, and Meta-Analysis. New York, NY: Routledge.
Dunlap, W. P. (1994). Generalizing the common language effect size indicator to bivariate normal correlations. Psychological Bulletin, 116(3), 509-511. doi: 10.1037/0033-2909.116.3.509
Dunlap, W. P., Cortina, J. M., Vaslow, J. B., & Burke, M. J. (1996). Meta-analysis of experiments with matched groups or repeated measures designs. Psychological Methods, 1, 170-177.
Elis, P. (2010). The Essential Guide to Effect Sizes: Statistical Power, Meta-Analysis, and the Interpretation of Research Results. Cambridge: Cambridge University Press.
Fritz, C. O., Morris, P. E., & Richler, J. J. (2012). Effect size estimates: Current use, calculations, and interpretation. Journal of Experimental Psychology: General, 141(1), 2-18. https://doi.org/10.1037/a0024338
Furukawa, T. A., & Leucht, S. (2011). How to obtain NNT from Cohen's d: comparison of two methods. PloS one, 6, e19070.
Hattie, J. (2009). Visible Learning. London: Routledge.
Hedges, L. & Olkin, I. (1985). Statistical Methods for Meta-Analysis. New York: Academic Press.
Klauer, K. J. (2001). Handbuch kognitives Training. Göttingen: Hogrefe.
Lakens D (2013) Calculating and reporting effect sizes to facilitate cumulative science: a practical primer for t-tests and ANOVAs. Frontiers in Psychology. doi: 10.3389/fpsyg.2013.00863
McGraw, K. O., & Wong, S. P. (1992). A common language effect size statistic. Psychological bulletin, 111(2), 361-365.
Morris, S. B., & DeShon, R. P. (2002). Combining effect size estimates in meta-analysis with repeated measures and independent-groups designs. Psychological Methods, 7(1), 105-125. https://doi.org/10.1037//1082-989X.7.1.105
Morris, S. B. (2008). Estimating Effect Sizes From Pretest-Posttest-Control Group Designs. Organizational Research Methods, 11(2), 364-386. http://doi.org/10.1177/1094428106291059
Rosenthal, R. (1994). Parametric measures of effect size. In H. Cooper & L. V. Hedges (Eds.), The Handbook of Research Synthesis (231-244). New York, NY: Sage.
Peterson, R. A., & Brown, S. P. (2005). On the use of beta coefficients in meta-analysis. The Journal of Applied Psychology, 90 (1), 175-181. https://doi.org/10.1037/0021-9010.90.1.175
Rosenthal, R. & DiMatteo, M. R. (2001). Meta-Analysis: Recent Developments in Quantitative Methods for Literature Reviews. Annual Review of Psychology, 52(1), 59-82. doi:10.1146/annurev.psych.52.1.59
Rosenthal, R., & Rubin, D.B. (1982). A simple general purpose display of magnitude of experimental effect. Journal of Educational Psychology, 74, 166-169.
Thalheimer, W., & Cook, S. (2002, August). How to calculate effect sizes from published research articles: A simplified methodology. Retrieved March 9, 2014 from http://work-learning.com/effect_sizes.htm.
Zitierfähige Quelle:
Lenhard, W. & Lenhard, A. (2022). Berechnung von Effektstärken. Abgerufen unter: https://www.psychometrica.de/effektstaerke.html. Psychometrica. DOI: 10.13140/RG.2.2.17823.92329

Jetzt erhältlich:
ELFE II - Ein Leseverständnistest für Erst- bis Siebtklässler
Beachten Sie auch unsere zusätzlich erschienenen
ELFE-II Normen für Kinder mit Migrationshintergrund.