Site menu:

cNORM - Generating Norm Tables
In addition to the pure modeling functions, cNORM also contains functions for generating norm tables, retrieving the normal score for a specific raw score and vice versa.
predictNorm
The 'predictNorm' function returns the normal score for a specific raw score (e.g., raw = 15) and a specific age (e.g., a = 4.7). The normal scores has to be limited to a minimum and maximum value in order to take into account the limits of model validity.
predictNorm(15, 4.7, model, minNorm = 25, maxNorm = 75)
predictRaw
The 'predictRaw' function returns the predicted raw score for a specific normal score (e.g., T = 55) and a specific age (e.g., a = 4.5).
predictRaw(55, 4.5, model, minRaw = 0, maxRaw = 28)
# ... or a matrix, if you like ...
predictRaw(c(45, 50, 55), c(2.5, 3, 3.5, 4, 4.5), model)
normTable
The 'normTable' function returns the corresponding raw scores for a specific age (e.g., a = 3) and a pre-specified series of normal scores. The parameter 'step' specifies the distance between two normal scores.
normTable(3, model, minRaw = 0, maxRaw = 28, minNorm=30.5, maxNorm=69.5, step = 1)
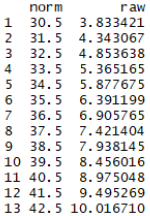
rawTable
The function 'rawTable' is similar to 'normTable', but reverses the assignment: The normal scores are assigned to a pre-specified series of raw scores at a certain age. This requires an inversion of the regression function, which is determined numerically. Specify reliability and confidence coefficient to automatically calculate confidence intervals:
rawTable(3.5, model, minRaw = 0, maxRaw = 28, minNorm = 25, maxNorm = 75, step = 1)
# generate several raw tables
table <- rawTable(c(2.5, 3.5, 4.5), m, minRaw = 0, maxRaw = 28)
You need these kind of tables if you want to determine the exact percentile or the exact normal score for all occurring raw scores.
 |
Model Validation |
Beta-Binomial Models |
 |