Site menu:

Switch to German language

cNORM - Modeling


We now want to find a regression model that models the original data as closely as possible with as few predictors as possible. We however want to smooth out noise from the original norm data, which can be due to the random sampling process or violations of representativeness. Internally, this is done through the 'bestModel' function, which is used by the general 'cnorm()' function. You can use this function in different ways: If you specify Radjusted2, then the regression function will be selected that meets this requirement with the smallest number of predictors. You can however also specify a fixed number of predictors. Then the model is selected that achieves the highest Radjusted2 with this specification. To select the best model, cNORM uses the 'regsubset' function from the 'leaps' package. As we do not know beforehand, how well the data can be modeled, we start with the default values (k = 5, t = 3 and Radjusted2 = .99):

model <- cnorm(raw = elfe$raw, group = elfe$group)

The function prints the following result:

Final solution: 3
R-Square Adj. amounts to 0.990812753080448
Final regression model: raw ~ L3 + L1A1 + L3A3
Beta weights are accessible via 'model$coefficients':

(Intercept)

L3

L1A1

L3A3

-1.141915e+01

2.085614e-05

1.651765e-01

-5.911150e-07


Regression formula:
[1] "raw ~ -11.4191452286606 + (2.08561440071111e-05*L3) + (0.165176532450589*L1A1) + (-5.9111502682762e-07*L3A3)"

Use 'plotSubset(model)' to inspect model fit

Fine! The determined model already exceeds the predefined threshold of Radjusted2 = .99 with only three predictors (plus intercept). The function as well returns the coefficients and the complete regression formula, which - as was specified - captures more than 99% of the variance in the data set.

The returned object 'model' contains both the data (model$data) and the regression model (model$model). If you want to have a look at the selection procedure, all the information is available in 'model$model$subsets'. The variable selection process per step is listed in 'outmat' and 'which'. There, you can find the R2, Radjusted2, Mallow's Cp and BIC as well. The regression coefficients for the selected model are available ('model$model$coefficients'), as well as the fitted scores ('model$model$fitted.values') and all other information. You can print a table with this information using the following code:

print(model)

Furthermore, information about the change of Radjusted and other information criteria (Mallow's Cp or BIC) depending on the number of predictors (with fixed k) can also be graphically inspected. Please use the following command to do this:

plot(model, "subset", type = 0)

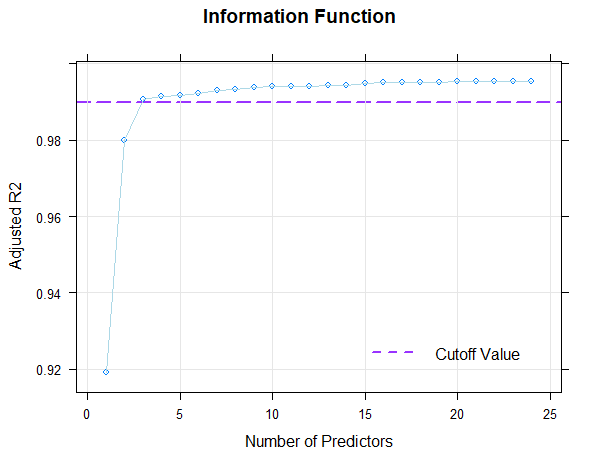
The figure displays Radjusted2 as a function of the number of predictors by default. Alternatively, you can also plot log-transformed Mallow's Cp (type = 1) or BIC (type = 2) as a function of Radjusted2.

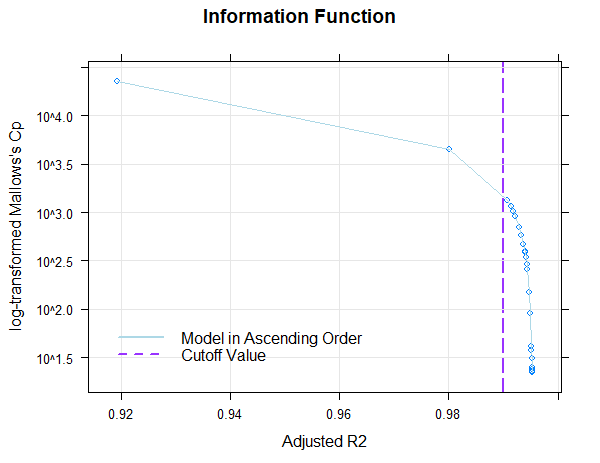
The figure shows that the default value of Radjusted = .99 is already achieved with only three predictors. The inclusion of further predictors only leads to small increases of Radjusted or to small decreases of Mallow's Cp. Where the dots are close together, the inclusion of further predictors is of little use. To avoid over-fitting, a model with as few predictors as possible should therefore be selected from this area.

The model with three predictors seems to be suitable. Nevertheless, the model found in this way must still be tested for plausibility using the means described in Model Validation. Above all, it is necessary to determine the limits of model validity. If a model turns out to be suboptimal after this model check, Radjusted2, the number of predictors or, if necessary, k should be chosen differently.



Repeated Cross-Validation

Indeed, the aim of the modeling process is not to capture the maximum variance in the observed data, but instead to retrieve models that predict the (probably unknown) population distribution. Fitting the model too closely to the training data is likely to result in an overfit. To avoid this and to estimate, how well the fitting can be carried out, you need to do a cross validation of the modeling. cNORM helps in selecting the number of terms for the model by doing repeated cross validation with 80 percent of the data as training data and 20 percent as the validation data. The cases are drawn randomly but stratified by norm group. Successive models are retrieved with increasing number of terms and the RMSE of raw scores (fitted by the regression model) is plotted for the training, validation and the complete dataset. Additionally to this analysis on the raw score level, it is possible to estimate the mean norm score reliability and crossfit measures.



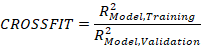
A Crossfit higher than 1 is a sign of overfitting. Value lower than 1 indicate an underfit due to a suboptimal modeling procedure, i. e. the method may not have captured all the variance of the observed data it could possibly capture. Values around 1 are ideal, as long as the raw score RMSE is low and the norm score validation R2 reaches high levels. As a suggestion for real psychometric tests:

The following example was generated on the basis of the elfe dataset with 10 repetitions and up to a maximum number of 10 terms in the regression function:

model <- cnorm(raw = elfe$raw, group = elfe$group)
cnorm.cv(model$data, repetitions = 10, max = 10)

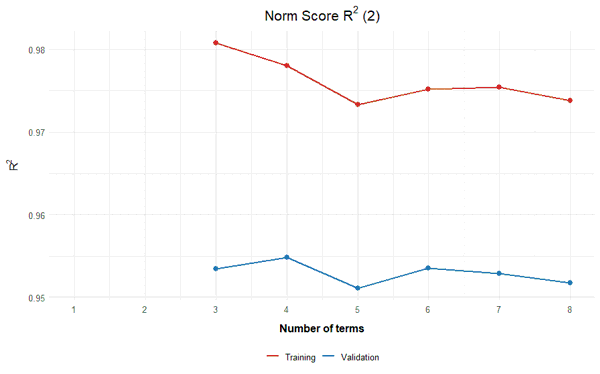
The results support the decision in the example above to include three terms in the regression function (+ Intercept). Adding more terms neither leads to a lower raw score RMSE nor to an increase in norm score R2 in the validation data. Including more terms simply results in an overfit. As long as there are no intersecting percentile curves in plotPercentiles, it is advisable to stay with that number of terms.



Weighting
 Model Validation