Site menu:

cNormj - Continuous Norming with cNORM in Jamovi
Jamovi is a very intuitive, free and open source statistical software. We have contributed the module "cNORMj" to the Jamovi software library, which offers you the essential cNORM functionality to generate norm scores for single groups or to apply regression-based continuous norming.
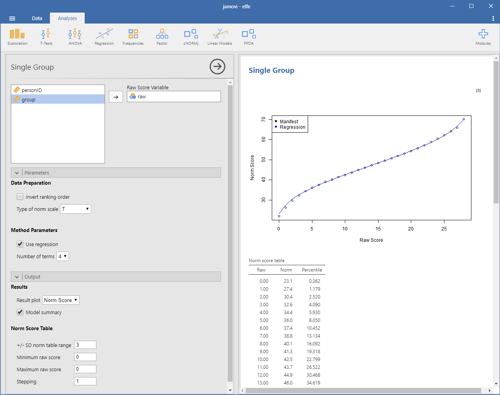
Norm score generation for single groups
This module estimates norm scores for raw scores within single groups and compiles norm tables. It is based on the Rankit procedure and inverse normal transformation. In order to smooth the norm score data and to close the missings, the functional relationship between raw score and norm score is modeled via polynomial regression up to power 5, using the cNORM package (W. Lenhard, Lenhard & Gary, 2018).
Please specify the raw score variable to obtain the norm table. Additional options:
- Data Preparation
- Invert ranking order: Please activate this option to set the ranking order to 'descending'. In this case, the highest values receive the lowest norm scores.
- Type of norm scale: You can compute T, IQ, z, PISA (m = 500, sd = 100) and Wechsler (m = 10, sd = 3) scales.
- Use regression: Per default, the module uses regression to model the relationship between raw and norm score. If this option is deactivated, it simply reports the manifest percentiles and norm scores on the basis of an inverse normal transformation of the percentiles (bindings are addressed via RankIt).
- Output
- Result plot: The plot is either set to norm scores or percentiles (cumulative function).
- Model summary: This gives you a report on the regression model.
- Norm table range: Restricts the norm score generation to +/- SD. Usually, it is not advisable to go beyond 3 SD, unless you have a really large dataset. For IQ scores this would result in an interval of IQ 55 to 145.
- Minimum raw score and Maximum raw score: You can specify the boundaries of the generated norm score table. Please note that this option is only taken into account, if the maximum score is higher than the minimum score, otherwise, the minimum and maximum raw scores from the data are used.
- Stepping: This option sets the granularity of the norm score table.
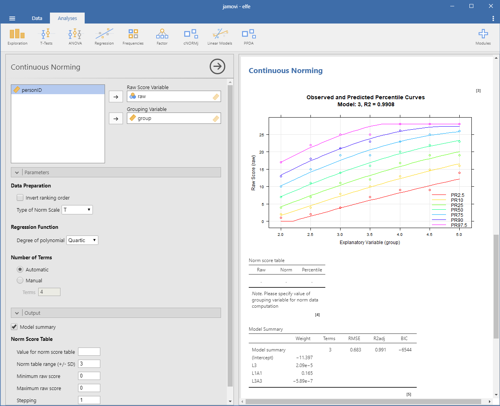
Continuous Regression-Based Norming
The module estimates continuous norm scores by modeling the functional relationship between raw scores (raw), norm scores (L) and the grouping variable (A; e. g. age, schooling duration ...) using the cNORM package (W. Lenhard, Lenhard & Gary, 2018). The modeling procedure minimizes the error variance contained in the norm scores. It requires smaller samples sizes compared to conventional norming, closes gaps within and between the norm tables and smoothes sampling errors.
Select a model with a low number of terms while preserving a high R2 of the model. Avoid intersecting percentile curves. The module gives you the following options:
- Data Preparation
- Invert ranking order: Please activate this option to set the ranking order to 'descending'. In this case, the highest values receive the lowest norm scores.
- Type of norm scale: You can compute T, IQ, z, PISA (m = 500, sd = 100) and Wechsler (m = 10, sd = 3) scales.
- Degree of polynomial: cNORM uses polynomial regression based on Taylor polynomials to retrieve the continuous norm score models. The degree specifies the power parameter and thus, which higher order relations are modeled. Quartic polynomials (power parameter 4) usually capture most of the variance in psychometric data, but it is advisable to reduced the parameter in smaller datasets to avoid overfitting.
- Number of terms: cNORM tries to find an optimal solution but it might be necessary to fine tune the model. Please vary the number of terms and use visual inspection of the percentile plot to identify good model solutions.
- Output
- Model summary: This gives you a report on the regression model. 'A' in the function refers to the grouping variable 'L' to the norm score. raw ~ L2 + L2A4 would thus mean, the raw score is predicted by the squared norm score and an interaction term of norm score (power 2) and grouping variable (power 4).
- Value for norm score table: Since the models are continuous, you explicitly need to specify the value for generating a specific norming table. In the example above, reading comprehension test data for grade 2 to 5 were used. For example, to generate a table for the first quarter of grade 3 (grouping variable 2.0 to 2.25), you could set it to the mid interval and thus specify a value of 2.125.
- Norm table range: Restricts the norm score generation to +/- SD. Usually, it is not advisable to go beyond 3 SD, unless you have a really large dataset. For IQ scores this would result in an interval of IQ 55 to 145.
- Minimum raw score and Maximum raw score: You can specify the boundaries of the generated norm score table. Please note that this option is only taken into account, if the maximum score is higher than the minimum score, otherwise, the minimum and maximum raw scores from the data are used.
- Stepping: This option sets the granularity of the norm score table.
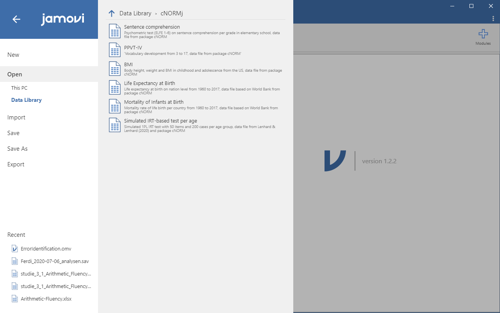
Sample Datasets
The cNORMj module includes the dataset from the cNORM package. You can use these to get accustomed to the analyses. To load the dataset, please click on the burger menu at the top left, select 'Open' and you will find the datasets in 'Data Library' in the folder 'cNORMj'.
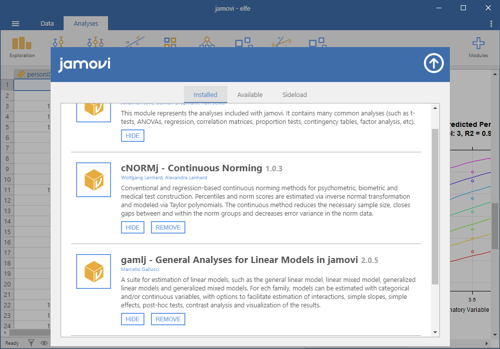
Installation
The 'cNORMj' module is available via the Jamovi library for all platforms. Please click on the 'Modules' option on the top right. You will find a library for the installation and management of the modules. You can as well download the module for Win64 and install it manually via 'Sideload'.
| Version | Name | Date |
| Binary Package (Windows, 64 Bit) | cNORMj Module (v. 1.0.3) | 12/07/2020 |
 |
Webinterface |
Frequently Asked Questions |
 |