Site menu:

cNORM - Generierung kontinuierlicher Testnormen
Alexandra Lenhard, Wolfgang Lenhard & Sebastian Gary
cNORM ist ein R-Package (A. Lenhard, Lenhard & Gary, 2018), welches zur Generierung kontinuierlicher Testnormen und zur Überprüfung der Modellpassung verwendet werden kann. Es basiert auf dem Ansatz von A. Lenhard, Lenhard, Suggate und Segerer (2016).
Die Methode, die hierbei verwendet wird, wurde ursprünglich zur Generierung kontinuierlicher Alters- oder Klassennormen bei psychometrischen Leistungstests entwickelt (z. B. Wortschatzentwicklung, A. Lenhard, Lenhard, Segerer und Suggate, 2015; Schriftspracherwerb, W. Lenhard, Lenhard und Schneider, 2017). Sie kann aber überall zum Einsatz kommen, wo psychologische (z. B. Intelligenz), physiologische (z. B. Körpergewicht) oder andere Testdaten von kontinuierlichen oder auch diskreten explanatorischen Variablen (z. B. Geschlecht, Testform usw.) abhängen. Zudem kann es auch für konventionelle Normdatengenerierung bei einzelnen Gruppen verwendet werden, also ohne Modellierung in Abhängigkeit weiterer Variablen.
Die Perzentilkurven werden mithilfe des Packages in Abhängigkeit von der explanatorischen Variable (also z. B. vom Alter oder der Beschulungsdauer) geschätzt. Dieses Vorgehen hat die folgenden Vorteile:
- Dadurch, dass das Modell anhand der Gesamtstichprobe optimiert wird, werden kleine Abweichungen von der Repräsentativität bei einzelnen Teilstichproben, die durch das Ziehen von Zufallsstichproben bedingt sind, insgesamt herausgemittelt (A. Lenhard, Lenhard & Gary, 2019).
- Lücken zwischen verschiedenen diskreten Stufen der explanatorischen Variable werden geschlossen. So können z.B. bei Schulleistungstests oder Intelligenztests Normtabellen nicht nur für den Erhebungszeitpunkt (z. B. Mitte oder Ende des Jahres), sondern zu einem beliebigen Zeitpunkt des Schuljahres oder zu einem beliebigen Alter mit der gewünschten Genauigkeit erstellt werden.
- Für die Ermittlung eines Normdatenpunktes wird nicht nur ein Jahrgang oder eine Klasse, sondern immer die gesamte Stichprobe herangezogen. Deshalb wird im Vergleich zu konventioneller Normierung selbst dann eine höhere Normierungsgüte erzielt, wenn wesentlich kleinere Stichproben verwendet werden (W. Lenhard & Lenhard, 2020).
- Die Grenzen der Modellpassung können grafisch und auch analytisch bewertet werden. So ist es bespielsweise möglich zu ermitteln, an welchen Stellen das Modell stark von den manifesten Daten abweicht oder an welchen Stellen starke Boden- oder Deckeneffekte auftreten. Damit kann präzisiert werden, an welchen Stellen die numerisch ermittelten Werte des Testverfahrens nicht mehr sinnvoll interpretiert werden können.
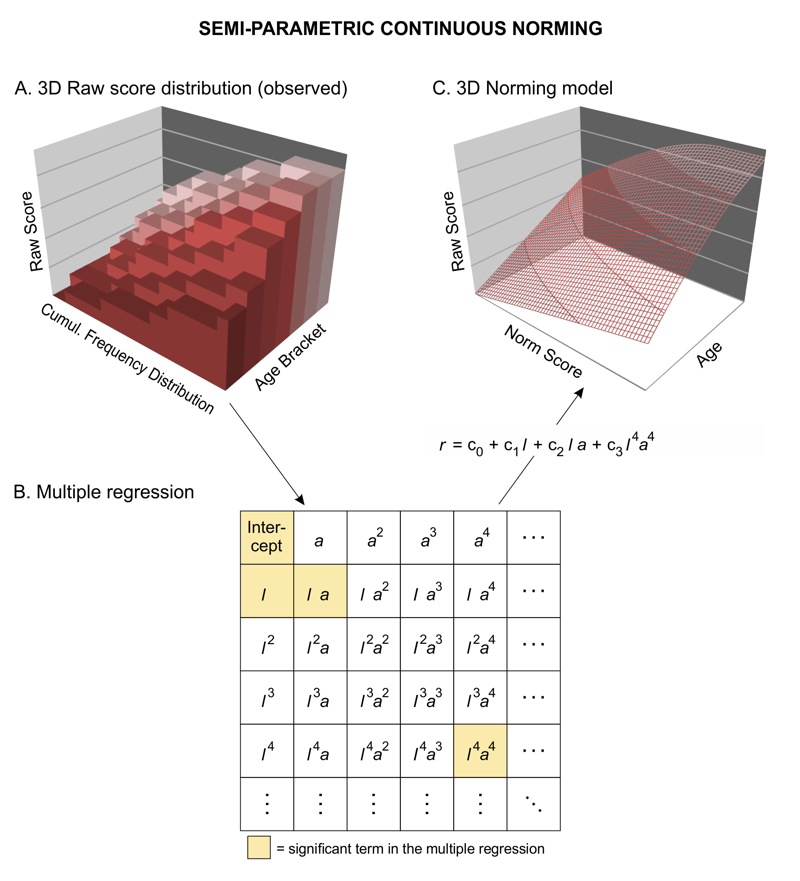
- cNORM benötigt keine Annahmen über die Rohwertverteilung. Die Daten können deshalb bei relativ kleinen Stichproben (< 100 pro Altersgruppe oder Klassenstufe) oder schiefen Verteilungen in der Regel präziser modelliert werden als mit parametrischen Verfahren (A. Lenhard, Lenhard & Gary, 2019). Dies gilt vor allem für diejenigen Bereiche, die relativ stark vom Mittelwert abweichen, oft aber eben genau jene Bereiche darstellen, die in der diagnostischen Praxis die höchste Relevanz besitzen. Dabei greift cNORM auf Taylor-Polynome zurück und modelliert die Zusammenhänge zwischen Rohwert, Alter und Fähigkeit, Rohwert als Anpassung einer Hyperfläche:
- Im Falle nicht repräsentativer Stichproben lassen sich mittels Iterative Proportional Fitting (Raking) Gewichte ermitteln, die die Auswirkungen der Nicht-Repräsentativität reduzieren.
Weitere Informationen zur Normierungsgüte von cNORM im Vergleich zu parametrischen kontinuierlichen Normierungsverfahren, wie sie in vielen wichtigen Intelligenzverfahren (z. B. WISC-V, WPPSI-IV, KABC-II, IDS-2) verwendet werden, finden Sie hier. Es handelt sich dabei um eine Simulationsstudie, in der wir auch darauf eingehen, wie unseres Erachtens die Güte von Normierungen generell nachgewiesen und in Testhandbüchern dokumentiert werden sollte.
Den Hintergrund unserer Methode finden Sie in der mathematischen Herleitung kurz beschrieben.
Auf den folgenden Seiten zeigen wir Ihnen die notwendigen Schritte bei der Anwendung des R-Packages anhand des Untertests Satzverständnis aus dem ELFE 1-6 Leseverständnistest (W. Lenhard & Schneider, 2006). Im Wesentlichen müssen fünf Schritte durchgeführt werden:
- Installation des R-Packages
- Datenaufbereitung
- Gewichtung
- Modellierung
- Validierung des Modells
- Generierung von Normtabellen
- Grafische Benutzeroberfläche im Browser oder als Jamovi Module
Auf einen Blick
Eine Kurzanleitung zu den wesentlichen cNORM-Funktionen:
## Beispielcode für die Modellierung eines Datensatzes
library(cNORM)
# Starten Sie die grafische Benutzeroberfläche (Shiny erforderlich).
# Die GUI enthält die wichtigsten Funktionen. Für spezielle Fälle
# verwenden Sie bitte cNORM auf der Konsole.cNORM.GUI()
# Verwendung der Syntax in der Konsole: Die Funktion 'cnorm'
# führt alle Schritte automatisch durch. Bitte spezifizieren Sie
# die Rohwert- und die Gruppierungsvariable.
# Das resultierende Objekt enthält die gerankten Daten über object$data
# und das Modell über object$model.cnorm.elfe <- cnorm(raw = elfe$raw, group = elfe$group)
# Darstellung der verschiedener Modellpassungen in Abhängigkeit der
# Anzahl der Prädiktorenplot(cnorm.elfe, "subset", type=0) # plot R2
plot(cnorm.elfe, "subset", type=3) # plot MSE# HINWEIS: An dieser Stelle wählen Sie normalerweise ein gut
# passendes Modell aus und wiederholen den Prozess mit einer
# festen Anzahl von Termen, z. B. vier. Vermeiden Sie Modelle
# mit einer hohen Anzahl von Termen:cnorm.elfe <- cnorm(raw = elfe$raw, group = elfe$group, terms = 4)
# Potenzen des Alters lassen sich getrennt über den Parameter
# 't' angeben. Meist reicht ein kurvlinearer Alterszusammenhang.
# 'k' spezifiziert dagegen die Potenz der Lokation. Hier kann
# dagegen höher gegangen werden.cnorm.elfe <- cnorm(raw = elfe$raw, group = elfe$group, k = 5, t = 3)
# Visuelle Inspektion der Perzentilkurven des angepassten Modells
plot(cnorm.elfe, "percentiles")
# Visuelle Inspektion der beobachteten und angepassten Roh- und Normwerte
plot(cnorm.elfe, "norm")
plot(cnorm.elfe, "raw")# Um zu prüfen, wie andere Modelle abschneiden, plotten Sie Serien von
# Perzentilplots mit aufsteigender Anzahl von Prädiktoren, in diesem
# Beispiel bis zu 14 Prädiktoren.plot(cnorm.elfe, "series", end=14)
# Kreuzvalidierung der Anzahl der Terme mit 20 % der Daten für die
# Validierung und 80 % für das Training. Aufgrund der Zeitintensität
# sind im Beispiel die Terme 10 beschränkt, bei 3 Wiederholungencnorm.cv(cnorm.elfe$data, max=10, repetitions=3)
# Kreuzvalidierung mit vordefinierten Termen, z. B. eines bereits
# bestehenden Modellscnorm.cv(cnorm.elfe, repetitions=3)
# Normtabelle erstellen (hier für Klasse 3, 3.2, 3.4, 3.6)
normTable(c(3, 3.2, 3.4, 3.6), cnorm.elfe)
# Umgekehrt: Darstellung der Rohwerttabelle (für Klasse 3) mit
# 90%-Konfidenzintervallen für einen Test mit einer Reliabilität von .94rawTable(3, cnorm.elfe, CI = .9, reliability = .94)
# cNORM kann auch für die konventionelle Normierung verwendet werden.
# In diesem Fall muss die Gruppenvariable beim Ranking der Daten auf
# FALSE gesetzt werden. Bitte verwenden Sie beim Generieren der
# Tabellen einen beliebigen Wert für das Alter.d <- rankByGroup(elfe, raw="raw", group=FALSE)
d <- computePowers(d)
m <- bestModel(d)
rawTable(0, model = m)# Vignette aufrufen
vignette("cNORM-Demo", package = "cNORM")
vignette("WeightedRegression", package = "cNORM")
| Installation |
 |
Nutzung von CNORM/Lizensierung
cNORM ist unter GNU Affero General Public License v3 (AGPL-3.0) lizensiert. Dies bedeutet, dass urheberrechtlich geschützte Teile von cNORM in kommerziellen und nicht-kommerziellen Projekten kostenlos verwendet werden dürfen, sofern die Projekte ebenfalls unter AGPL stehen, den eigenen Source-Code verfügbar machen und cNORM korrekt zitieren. Vom Urheberschutz und der Lizenz sind z. B. die Vervielfältigung und Verbreitung von Quellcode oder von Teilen des Quellcodes von cNORM oder von mit cNORM erstellte Grafiken gedeckt. Auch die Einbindung des Paketes in eine Serverumgebung, um auf die Funktionalität der Software zugreifen zu können (z. B. für online-Abfragen von Normen), unterliegt dieser Lizenz. Eine mit cNORM ermittelte Regressionsfunktion unterliegt hingegen keinem urheberrechtlichen Schutz und darf für kommerzielle oder nicht kommerzielle Projekte frei verwendet werden. Falls Sie cNORM in einer Weise einsetzen möchten, die nicht mit den Bedingungen der AGPL-3.0-Lizenz vereinbar ist, dann kontaktieren Sie uns gerne, um individuelle Bedingungen auszuhandeln.
Sollten Sie cNORM für wissenschaftliche Publikationen einsetzen wollen (hierzu zählen auch psychometrische oder biometrische Testverfahren), dann bitten wir außerdem um Quellenangabe.
Literaturangaben
| CDC (2012). National Health and Nutrition Examination Survey: Questionaires, Datasets and Related Documentation. verfügbar unter: https://wwwn.cdc.gov/nchs/nhanes/OtherNhanesData.aspx (date of retrieval: 25/08/2018) |
| Lenhard, A., Lenhard, W. & Gary, S. (2019). Continuous norming of psychometric tests: A simulation study of parametric and semi-parametric approaches. PLoS ONE, 14(9), e0222279. https://doi.org/10.1371/journal.pone.0222279 |
| Lenhard, A., Lenhard, W., Segerer, R. & Suggate, S. (2015). Peabody Picture Vocabulary Test - Revision IV (Deutsche Adaption). Frankfurt a. M.: Pearson Assessment. |
| Lenhard, A., Lenhard, W., Suggate, S. & Segerer, R. (2016). A continuous solution to the norming problem. Assessment, Online first, 1-14. doi: 10.1177/1073191116656437 |
| Lenhard, W., Lenhard, A. & Schneider, W. (2017). ELFE II - Ein Leseverständnistest für Erst- bis Siebtklässler. Göttingen: Hogrefe. |
| Lenhard, W. & Schneider, W. (2006). ELFE 1-6 - Ein Leseverständnistest für Erst- bis Sechstklässler. Göttingen: Hogrefe. |
| The World Bank (2018). Mortality rate, infant (per 1,000 live births). Data Source available https://data.worldbank.org/indicator/SP.DYN.IMRT.IN (date of retrieval: 02/09/2018) |
| The World Bank (2018). Life expectancy at birth, total (years). Data Source World Development Indicators available https://data.worldbank.org/indicator/sp.dyn.le00.in (date of retrieval: 01/09/2018) |
| Lenhard, W., & Lenhard, A. (2020). Improvement of Norm Score Quality via Regression-Based Continuous Norming. Educational and Psychological Measurement, Online First, 1-33. https://doi.org/10.1177/0013164420928457 |
Zitierfähige Quelle für diese Seite:
Lenhard, A., Lenhard, W. & Gary, S. (2018). cNORM - Generierung kontinuierlicher Testnormen. Abgerufen unter: https://www.psychometrica.de/cNorm.html. Dettelbach: Psychometrica.